·
Media
aritmética o media,(x):
Media
aritmética o media,(x):
Se
calcula para variables cuantitativas. Es la suma de todos los valores de la
variable observada entre el total de observaciones. La fórmula es:
x= Ʃx/n
Para calcular
la media utilizamos como valor de referencia de cada intervalo su marca de
clase: se calcula una media aritmética
ponderada que se calcula sumando la marca de clase por la frecuencia
absoluta, entre N.
x= Ʃmc (marca de clase)fi /n
Ejemplo:
Peso en Kg
|
fi(Frecuencia absoluta)
|
EFi(frecuencia absoluta
acumulada)
|
hi(frecuencia relativa)
|
Hi (frecuencia relativa
acumulada)
|
[3.3-3.8]
Mc= 3.5
|
3
|
3
|
0.075
o 7,5%
|
0.075
o 7,5 %
|
(3.8-4.3]
Mc=4.0
|
8
|
11
|
0.2
o 20%
|
0.275
o 27,5 %
|
(4,3-4.8]
Mc=4.5
|
14
|
25
|
0.35
o 35%
|
0.625
o 62,5%
|
(4.8-5.3]
Mc=5.0
|
6
|
31
|
0.15
o 15%
|
0.775
o 77.5%
|
(5.3-5.8]
Mc=5.5
|
4
|
35
|
0.1
o 10%
|
0.875
o 87,5 %
|
(5.8-6.3]
Mc=6.0
|
5
40
|
40
|
0.125 o
12,5%
100%
|
1
o 100%
|
Mediana:
medida de posición y central
Es el valor de la observación tal que deja a un 50% de los
datos menor y otro 50% de los datos
mayor.
-
Si el número de observaciones es impar el valor será justamente la observación que ocupa la posición
(n+1/2)
-
Si el número de observaciones es par, el valor de la mediana corresponde a la media entre los dos
valores centrales, es decir, la media entre la observación n/2 y la observación
(n/2)+1.
·
Moda: Es el valor
con mayor frecuencia (que más veces se repite). Si hay más de una se dice
que la muestra es bimodal (dos modas) o multimodal (más de dos modas).
que la muestra es bimodal (dos modas) o multimodal (más de dos modas).
Si los
datos están agrupados, se habla de clase
modal.
2. Medidas de Posición o Cuantiles
Se calculan para variables cuantitativas.
Los cuantiles más usuales son los percentiles, los deciles y
los cuartiles, según dividan la
muestra ordenada en 100 (perciles), 10 (deciles) ó 4 partes (cuartiles),
respectivamente.
Aquí o dejo un vídeo explicativo de Youtube sobre dudas acerca de estos conceptos.
Aquí o dejo un vídeo explicativo de Youtube sobre dudas acerca de estos conceptos.
·
Rango o recorrido: Diferencia
entre el mayor y el menor valor de la muestra lXn-X1l
(valor absoluto).
·
Desviación media: Media aritmética de las distancias de cada
observación con respecto a la media de la muestra:
Para
datos agrupados:
·
Desviación típica o estándar: Esta es la
que más se emplea debido a que esta nos da un
mayor rango de error.
Para datos agrupados:
Para agrupados:
- Recorrido
intercuartílico: Diferencia entre el tercer y el primer cuartil
= lQ3-Q1l
- Coeficiente
de variación: Nos sirve para comparar la heterogeneidad de
dos series numéricas con independencia de las unidades de medidas. Se
expresa sin unidades. Se calcula
dividiendo la desviación típica y la media.
c.v.=s/
El C.V.
siempre va de 0 a 1.
Aquí o dejo un vídeo explicativo de Youtube sobre dudas acerca de estos conceptos.
Aquí o dejo un vídeo explicativo de Youtube sobre dudas acerca de estos conceptos.
Ejercicio:
Unas
enfermeras han registrado en el punto de vacunación las edades de nueve niños
que han sido vacunados durante una sesión, obteniéndose los siguientes datos:
3, 2, 4,
2, 1, 3, 5, 3 y 4 meses.
Calcular:
a. Media
aritmética:
b. Mediana=1
c. Moda=3
d. Rango o
recorrido
e. Varianza.
f.
Desviación típica.
g. Coeficiente
de variación.
4. Distribuciones Normales
En
estadística se llama distribución normal, distribución de Gauss o distribución
gaussiana, a una de las distribuciones de probabilidad de variable continua que
con más frecuencia aparece en fenómenos reales.
Las
distribuciones normales en un histograma aparece una especie de Campana, por
eso la campana de Gauss. Y es simétrica respecto de los valores de posición
central, es decir que la moda va a coincidir con la media y la mediana. Esta
curva se conoce como campana de Gauss.
5. Asimetrías
La
asimetría es al lado contrario al que vemos el pico (la moda), es decir si
vemos el pico hacia la derecha la asimetría es a la izquierda, y si la moda está
a la izquierda la asimetría esta hacia la derecha.
6. Tipificación de los valores y su relación con la campana de Gauss
Trabajamos
con una variable continua que:
-
Sigue
una distribución normal (TLC)
-
Tiene
mas de 100 unidades (LGN)
La tipificación nos permite conocer
si valor corresponde o no a esa distribución con frecuencia
Sabemos por la forma de la curva que:
La media coincide con lo más alto de
la campana: 8
La desviación típica es de 2 puntos:
-
El 50 % tienen
puntuaciones >8
-
El
50% tiene puntuaciones <8
-
Aproximadamente
el 68% puntúa entre 6 y 10
o
Media
+/- 1 desviación típica: 68%
8+/-1:
6-10
o
Media
+/- 2 desviación típica: 95%
4-12
o
Media
+/- 3 desviación típica: 99%
2-12
¿Qué
proporción de mujeres tiene una proporción de entre 4 y 10 en la escala?
Z= (4-8)/2= -1,5
Z2= (10-8)/2= 1
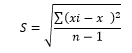
No hay comentarios:
Publicar un comentario